Basic Transformations

Geometric Interpretations

Many basic matrix transformations have simple geometric interpretations

Matrices can be used to perform:

  → Reflections

  → Rotations

  → Contractions

  → Expansions

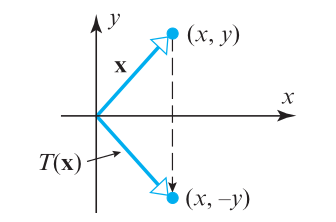
Vertical Reflection

\[ A = \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix}\]

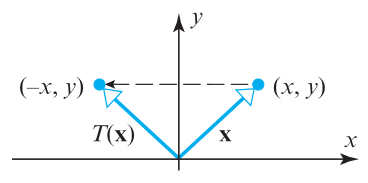
Horizantal Reflection

\[ A = \begin{bmatrix} -1 & 0 \\ 0 & 1 \\ \end{bmatrix}\]

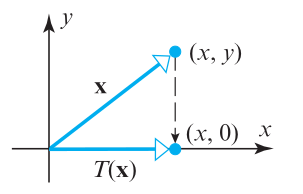
Projection

\[ A = \begin{bmatrix} 1 & 0 \\ 0 & 0 \\ \end{bmatrix}\]

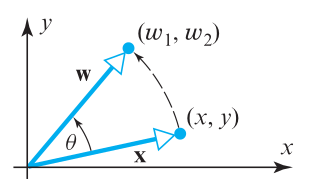
Rotations

\[ A = \begin{bmatrix} \cos(\theta) & -\sin(\theta)\\ \sin(\theta) & \cos(\theta)\\ \end{bmatrix}\]

Contractions

\[ A = \begin{bmatrix} k & 0 \\ 0 & m \\ \end{bmatrix}\]

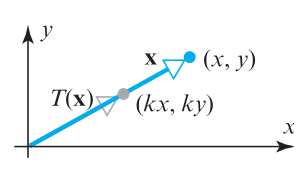
Composition of Transformations

When multiple transformations are applied, we have a composition

For example, applying transformations T_A and T_B is represented by:

\[ T_{BA} = T_{B} \circ T_{A}\]

As transformations are performed as matrix multiplications, so are compositions

Example

\[ T_{A} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix}\text{, } T_{B} = \begin{bmatrix} k & 0 \\ 0 & k \\ \end{bmatrix} \]

\[ T_{BA} = T_{B} \circ T_{A} = \begin{bmatrix} k & 0 \\ 0 & k \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} = \begin{bmatrix} k & 0 \\ 0 & -k \\ \end{bmatrix}\]

Eigenvalues and Eigenvectors

Definition

If A is a square matrix, then a vector x is called an eigenvector of A if Ax is a scalar multiple of x

In other words, if we have a vector x, and a scalar λ, such that:

\[ A\mathbf{x} = \lambda \mathbf{x} \]

Then, x is an eigenvector of A, and λ is its corresponding eigenvalue

Practical uses

Eigenvalues and eigenvectors have several uses in sciences and engineering:

  → Google's PageRank

  → Machine Learning

  → Data Compression

  → Data Science (reducing dimensions)

  → Solution of Differential Equations

Interpretation

When a vector x is multiplied by a matrix A, the result can change both its magnitude as well as direction

However, for eigenvectors, only the magnitude is changed

\[ A\mathbf{x} = \lambda \mathbf{x} \]

Characteristic Equation

λ is an eigenvalue of a matrix A if, and only if, it satisfies the equation:

\[ det(\lambda I - A) = 0 \]

This is called the characteristic equation of A

Calculating eigenvalues and eigenvectors

To find eigenvalues, one must solve the characteristic equation

\[ det(\lambda I - A) = 0 \]

Then, one needs to find, for each eigenvalue, its corresponding eigenvector by solving the system:

\[ (\lambda I - A)\mathbf{x} = 0 \]

Example

\[ A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \\ \end{bmatrix} \]

More Examples

\[ A = \begin{bmatrix} 4 & 1 \\ 2 & 3 \\ \end{bmatrix},\ A = \begin{bmatrix} 6 & -1 \\ 2 & 3 \\ \end{bmatrix} \]